논문 링크 : https://arxiv.org/pdf/1512.03385.pdf
Abstract
딥러닝에서 neural networks가 깊어질수록 성능은 더 좋지만 train이 어렵다는 것은 알려진 사실이다. 그래서 이 논문에서는 residual를 이용한 잔차학습 (residual learning framework)를 이용해서 깊은 신경망에서도 training이 쉽게 이뤄질 수 있다는 것을 보이고 방법론을 제시했다.
이 논문에서 ResNet은 더 optimize하기 쉽게 하고, 더 깊은 모델로 부터 쉽게 accuracy를 증가 시키며 더 깊에 쌓는 방법에 초점을 두며 데이터를 이용한 실험을 통해 증명한다.
VGG nets 보다 8배 깊은 152개의 layers를 가진 residual nets로 ImageNet을 학습하고 평가하여 3.57%라는 매우 작은 error를 보이며 VGGNet, GoogLeNet을 제치고 ILSVRC 2015에서 1위를 차지했다.
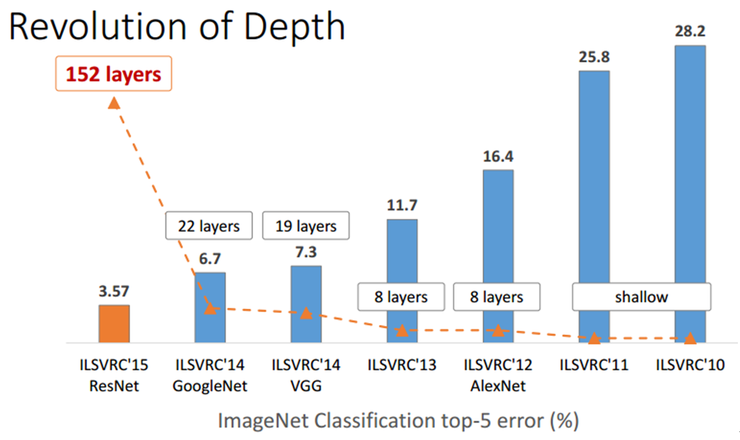
이외에도, CIFAR-10, COCO의 detection, segmentation등에 좋은 성능을 보여 매우 성능이 좋은 nets라는 것을 알 수 있다.
1. Introduction
DCNN(Deep Convolutional Neural Networks)은 이미지 분류 분야에 있어서 획기적인 발전을 이끌었다. 최근까지의 네트워크들은 depth가 중요한 요소로 여겨졌고, 더 깊은 모델일수록 기존보다 더 좋은 성능이 나온다고 것을 ImageNet challenging등의 여러 대회에서 보여줬다.
그래서 “depth를 늘리는 것만으로 쉽게 성능을 향상 시킬 수 있을까?”라는 의문을 갖은 ResNet팀은 망이 깊어지는 경우 어떤 결과가 나오는지 실험을 하였다. 짧은 시간에 실험하기 위해 ImageNet보다 작고 간단한 CIFAR-10 학습 데이터를 20-layer와 56-layer에 대해 비교 실험 하였다. 결과는 아래와 같다.
결과는 depth가 증가할 수록 어느 부분까지 성능이 향상되다 vanishing/exploding gradient 문제로 어느정도 선에 다다르면 성능이 떨어지는 모습을 보였다. 이러한 현상을 “degradation”이라고 하는데, 다시 말하면 depth가 증가함에 따라 accuracy가 포화(saturate)되어 degrade가 점점 빨라진다는 것이다. 이러한 degradation 문제는 overfitting이 원인이 아니라, Model의 depth가 깊어짐에 따라 training-error가 높아진다는 것이다.
이 문제는 normalized initialization, intermediate normalization layers를 통해 크게 개선되어 수십개의 layer를 가진 네트워크가 역전파와 함께 SGD에 수렴해 나가도록 한다.
Degradation은 모든 시스템이 optimize 하기 쉽지 않다는 것을 뜻하기 때문에 이 논문에서는 얕은 구조와 깊은 아키텍처를 고려해 본다. 이 논문에서 degradation 문제를 더 깊은 레이어가 쌓일 수록 optimize 하기 어렵기 때문에 일어나는 부작용으로 보고 해결책을 찾는것으로 보인다.
먼저 간단하게 미리 훈련된 얕은 모델에 identity mapping layer를 추가해봤지만 실험을 통해 좋은 solution이 아니라는 결과를 얻었다. 그래서 이 논문에서는 deep residual learning framework 라는 개념을 도입한다. 각 스택 레이어가 기본 매핑으로 바로 적합되는 것이 아니라 residual mapping에 적합하도록 만들었다.
기존 매핑이 H(x)이면 이 논문에서는 nonlinear layer 매핑인 F(x) = H(x) - x를 제시한다. 이를 전개하면 기존 매핑은 H(x) = F(x) + x 의 형태가 된다. 여기서 residual mapping이 기존 매핑보다 optimize 하기 쉽다는 것을 가정한다.
To the extreme, if an identity mapping were optimal, it would be easier to push the residual to zero than to fit an identity mapping by a stack of nonlinear layers.: 극단적으로 identity mapping이 optimal하면, nonlinear layer를 쌓아서 identity mapping을 맞추는 것 보다 residual을 0으로 만드는 것이 더 쉽다.
식 F(x) + x는 shortcut connection과 동일한데 이는 하나 또는 이상의 레이어를 skip하게 만들어준다. residual mapping에서 shortcut connection은 identity mapping 단순하게 수행하고, 그 출력을 다음 스택 레이어의 출력에 추가된다. Identity short connection은 추가적인 파라미터도 필요하지 않고 복잡한 곱셈 연산도 필요하지 않는 것이 장점이다. 또한 전체 네트워크는 역전파와 함께 SGD에 의해 end-to-end로 학습되고, 기존 라이브러리를 이용하여 간단히 구현 가능하다.
위의 내용을 그림으로 이해해보면 다음과 같다.

x 는 input인데 Model 인 F(x)라는 일련의 과정을 거치면서 자신(identity)인 x가 더해져서 output으로 F(x) + x 가 나오는 구조이다. (추가 : 개념적으로 보면 F(x)는 Model, relu는 function 이라고 한다.)
이제부터 실험적인 방법을 통해 degradation 문제를 보이고 이 논문의 방법을 평가하는 것이 나옵니다. 이 논문에서 보여주고자 하는 목표 두 가지는 다음과 같다.
1) Our extremely deep residual nets are easy to optimize, but the counterpart “plain” nets (that simply stack layers) exhibit higher training error when the depth increases; -> plain net과 다르게 residual net이 더 쉽게 최적화 된다.
2) Our deep residual nets can easily enjoy accuracy gains from greatly increased depth, producing results substantially better than previous networks. -> residual net이 더 쉽게 accuracy를 얻을 수 있다.
ImageNet classification dataset에서 ResNet팀은 152 layer residual net을 사용하여 VGGNet보다 낮은 복잡도로 top-5 error율이 3.57%로 놀라운 성능을 얻었으며 ILSVRC 2015 classification에서 1위를 차지했다.
2. Related work
Residual Representation
이미지 인식 분야에서 VLAD는 dictonary에 연관되게 residual vectors에 의해 인코딩되는 표현이며 Fisher Vector는 VLAD 확률적 버전으로 공식화 하였다.
Both of them are powerful shallow representations for image retrieval and classification.: 두 가지 모드 이미지 검색 및 분류에 있어서 강력한 얕은 표현이다. 여기서 vector 양자화에 있어서 residual vectors를 encoding하는 것이 기존의 vectors를 encoding하는 것 보다 더 효과적이라고 말한다.
또한 low-level vision과 computer graphics에서 Partial Differential Equations (PDEs) 해결을 위해 Multigrid method가 넓게 사용되었다. Multigrid 는 이산화 계층을 사용하여 미분 방정식을 풀기 위한 알고리즘이다.
An alternative to Multigrid is hierarchical basis preconditioning, which relies on variables that represent residual vectors between two scales.: multigrid의 대안으로 hierarchical basis preconditioning이 있는데 이는 2 scale 사이의 residual vector로 나타나는 변수에 의존한다.
이 대안은 잔류 특성을 모르는 일반적은 solution보다 훨씬 빠르게 수렴해 갑니다. 이 방법은 좋은 reformulation 이나 reconditioning이 최적화를 간단히 할 수 있다는 좋은 방법은 제안한다.
3. Deep Residual Learning
3.1 Residual Leraning
If one hypothesizes that multiple nonlinear layers can asymptotically approximate complicated functions, then it is equivalent to hypothesize that they can asymptotically approximate the residual functions, i.e., H(x) − x (assuming that the input and output are of the same dimensions): 앞서 말한 것과 같이 H(x)를 기존 매핑으로 간주하고 x가 input 일때 다수의 비선형 레이어가 복잡한 함수를 asymptotically 근사화 할 수 있다고 가정하면 잔차함수를 asymptotically 근사 할 수 있다는 가설과 같다고 한다.
즉, 복잡한 함수를 다수의 비선형 레이어가 근사시킬 수 있다면 잔차함수도 근사할 수 있다는 가설이다.
이에 대한 증명은 실험을 통해 이 논문에서 밝혔다.
3.2 Identity Mapping by Shortcuts
ResNet은 아무리 적게 쌓인 layers일지라도 residual learning을 적용한다. Fig.2에서 보인 block을 다음과 같이 정의한다.

여기서 x는 input, y는 output vectors, F(x,{Wi})는 학습될 residual mapping을 의미한다.
그림 2의 그림을 수식으로 나타내면 다음과 같다. F=W2σ(W1x)
여기서 σ 는 ReLU를 의미하고 biases는 notation을 간략화하기 위해 생략했다.
식 1은 사실 F = W2σ(W1x)를 간소화한 모양이다. weight w1과 함께 x는 relu함수 σ를 한 번 통과했고 다음 weight w2가 곱해진 모습이다. bias는 생략해서 나타냅니다. 이 때 x, F의 차원은 동일해야 하고, 식 2를 통해 차원에 맞게 shortcut connections를 통해 linear projection을 수행 할 수 있다.

앞서 나왔던 내용중에 extra parameter와 computational complexity가 추가적으로 필요없다는 것이 기존의 plain networks와 residual networks를 비교하는데 매우 중요하고 매력적인 요소가 될 것이다.
이어서 나올 실험들을 통해 identity mapping이 degradation 문제와 효율성의 문제를 충분히 해결할 수 있다는 것을 보여줄 것이고, Ws는 오직 차원을 맞추는데만 사용됩니다.
만약에 F가 Single layer라면 식 (1)은 linear layers와 유사한다: y=W1x + x F(x,Wi)는 multiple convolutional layers를 표현할 수 있다.
3.3 Network Architectures
Plain network와 residual network를 비교하기 위해 ImageNet의 data를 이용한다.
Plain Network
Plain Network는 가운데에 나타낸 것처럼 단순히 layers를 쌓기만한 그림이다.
Conv layers는 대부분 3X3 filters를 가지고 있고, 다음의 간단한 규칙을 따릅니다
- 각 layers는 같은 크기의 output feature map을 가지고, 같은 수의 filters를 갖는다.
- 만약에 feature map size가 반으로 줄어들었다면, layer당 time-complexity를 유지하기 위해 filters의 수는 두 배가 된다.
downsampling을 하기 위해서 stride가 2인 conv layers를 통과시킵니다. 그리고 네트워크는 global average pooling과 1000-way-fully-connected layer with softmax로 끝납니다. 이 모델은 VGG nets보다 filters의 수가 적고 VGG ent의 18%의 lower complexity를 가진다는 것이 장점이다.
Residual Network
위의 plain network에 기반하여, shortcut connections를 추가한 residual version ResNet이다. input과 output의 차원이 같다면 identity shortcuts는 바로 사용될 수 있다. 차원이 증가한다면 두 가지 경우를 생각해야한다.
- (A) shortcut은 계속 identity mapping을 하고, 차원을 증가시키기위해 zero-padding을 해야한다.(이 옵션이 왜 추가 파라미터가 필요없는지 설명해준다.)
- (B) 식 (2)에서 projection shortcut을 할 때 차원을 맞추기 위해 1X1 conv를 사용한다.
위 두 가지 options는 shortcuts이 feature map을 2 size씩 건너뛰기 때문에 stride를 2로 사용한다.
3.4 Implementation
ImageNet data에 적용시켜 다음과 같이 설정한다.
- image resize: 224 * 224
- Batch normalization(BN) 사용
- Initialize Weights
- SGD
- mini batch: 256
- Learning rate 0.1 (참고 : learning rate 설정에 대한 이론을 알고 싶으면 armijo rule 참고할 것, 딥러닝은 0.1,0.01,0.001의 정해진 수를 많이 씀)
- Iteration: 60 * 10^4
- weight decay: 0.0001
- momentum: 0.9
- No dropout
test 시에는 10-crop testing을 적용하였다. 10-crop이란 image에 대해 총 10번 잘라서 보는 것인데, 각 모서리에 대해 총 8번 중앙부에 2번 진행한다.

(큰 모서리 4번 + 작은 모서리 4번 + 작은 중앙 1 + 큰 중앙 1= 10 ) 그리고 최적의 결과에 fully convolutional을 적용했고, multiple scale에 대해서 점수를 평균화했다.
4. Experiments
4.1 ImageNet Classification
1,000 개의 class를 가진 ImageNet 2012 classification dataset 을 사용하였다. 128장의 training images를 사용하고, 평가를위해 5만장의 validation images를 사용하였다. 그리고 최종 결과를 내기위해 10만장의 test images를 사용하여 top 1 ~ 5의 error rate를 평가하였다.
Plain Networks
처음에는 18, 34-layer를 가지는 plain network로 평가했다.
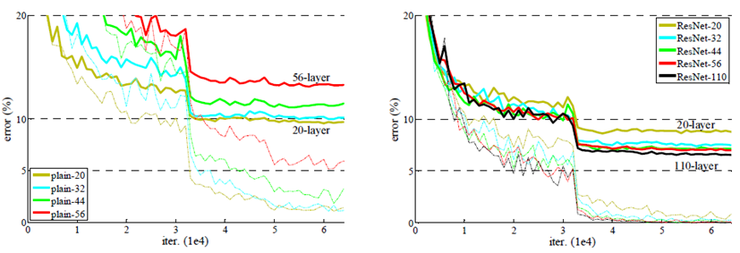
표 2를 보면 34-layer의 validation error가 18-layer의 error보다 높게 나왔다. 여기서 degradation의 문제를 관측했다. 그림 4를 보면 layer가 더많은 plain-34가 더 높은 training error를 보이는 것을 알 수 있다.
이러한 문제에 대해 optimization problem이 vanishing gradients때문에 일어났을 것이라고 생각하지는 않았다. 왜냐하면 BN을 통해 학습되었고 backward, forward 모두 문제가 없었기 때문이다. 그 말은 즉, 아직 34-layer plain nets이 경쟁력이 있다는 소리이다. 추측으로는 deep plain nets이 기하급수적으로 낮은 수렴률을 가지고 있어서 training error를 줄이는 영향을 준다는 것이다.
Residual Networks
그리고 18, 34-layer를 가지는 residual network를 평가했다.
모든 shortcuts을 위해서는 identity mapping을 사용했고, 차원증가를 위해서는 zero-padding을 사용했다. (옵션 A- 그래서 추가 파라미터가 없다)
표 2와 그림 4를 통해 얻을 결론을 정리하면 다음과 같다.
- 18-layer ResNet 보다 34-layer ResNet이 2.8%나 더 낮은 training error를 가진다. layer의 깊이가 증가할 때도 degradation problem 을 잘 조절했음을 보인다. 또한 그림 4에서 training error가 줄어들고 있고, validiation data에 대해 더 일반화를 잘하고 있다는 것을 알 수 있다. 이로써 degradation 문제를 잘 해결했다고 말할 수 있다.
- 표 2에서 34-layer plain net에 비교하여 34-layer ResNet은 3.5%나 더 낮은 error를 보인다(training error 감소 또한 성공적). 이 비교는 deep한 system의 residual을 학습하는 것이 더 효율적이라는 것을 증명해냈다.
- 그림 4를 보면 ResNet이 더 빠르게 수렴하는 모습을 볼 수 있다. net이 overly depp하지 않다면 여전히 SGD는 좋은 solution이지만 ResNet이 더 쉽게 최적화를 수행한다.
Identity vs Projection Shortcuts
앞서봤지만, identity shortcuts는 training에 도움이 된다는 것을 확인했다. 표 3을 통해 우리는 3가지 options를 비교할 수 있다.
- (A) 차원 증가를 위해 zero-padding을 사용하는 경우 (추가 파라미터 없음)
- (B) 차원 증가를 위해 projection shortcuts을 사용, (Ws) (다른 shortcuts은 identity)
- (C) 모든 shortcut들이 projection인 경우
표 3을 보면 3가지 옵션이 적어도 plain nets보다는 낫다는 것을 알 수 있다.
비교 결과 성능은 다음과 같다.
C > B > A
(B)가 (A)보다 조금 나은데 이는 (A)의 zero-padding과정에 residual learning이 없기 때문이라고 말한다.
(C)도 (B)보다 조금 좋은 성능을 보이는데, 이는 추가 파라미터가 많은 projection shortcuts에 의해 설명된 것이 성능에 기인했다고 말한다.
(A),(B),(C)의 차이가 작은걸 보면 projection shortcuts는 degradation 문제를 해결하는데는 필수적이진 않다는 것을 알 수 있다. 그래서 memory를 덜 잡아먹기위해서 (C)는 앞으로 사용하지 않는다.
Identity shortcuts는 아래 설명될 bottleneck architectures의 복잡성을 증가시키지 않는데 특히 중요하다.
Deeper Bottleneck Architectures
더 deep한 모델을 만들기 위해 2-layers가 아닌 3-layers를 쌓는다.
3-layers는 1X1 , 3X3, 1X1의 convolution이고, 1X1 layers는 차원을 감소하고 증가(복원)시켜, 더 작은 input/output 차원으로 Bottleneck을 일으킨다.
그림 5를 보면 두 개의 time complexity도 비슷하다.
앞서 말한 것 처럼 identity shortcut는 time complexity와 model size를 줄이는데 중요하다. 이 과정이 projection으로 바뀌게 되면 time complexity와 model size가 배가 된다. 따라서 identity shortcut이 bottleneck designs를 더 효율적으로 만들어준다.
- 50-layers ResNet: 기존 34-layer에 3-layer bottleneck block을 Table1의 50-layers을, option은 (B)를 택해서 차원을 증가시켰다.
- 101-layers and 152-layers ResNet: 위와 같은 option에서 depth만 증가시켰다. 확실이 기존의 34-layers보다 상당한 차이가지며 좋은 성능을 보였다. degradation의 문제는 찾지 못하고 깊이가 더 깊어짐에 따라 더 좋아지는 것을 목격했다.
Comparisons with State-of-the-art Methods
ResNet을 포함한 위에서 만들었던 6가지의 모델을 앙상블을 해서 error fmf 3.57%까지 줄였고 이 결과가 ILSVRC 2015에서 우승하였다.
4.2 CIFAR-10 and Analysis
ResNet 팀은 CIFAR-10에 대한 검증을 위해 망 구성을 약간 변형을 시켰다. 그 이유는 ImageNet(ILSVRC) 데이타의 경우는 224x224로 영상의 크기가 컸지만, CIFAR-10에 있는 영상이 32x32로 크기가 작기 때문이다. 검증 방식은 동일한 layer 수를 갖는 Plain과 Residual Network을 비교 실험하는 것이다.
ImageNet 데이타를 이용한 실험에서는 맨 처음 convolutional layer에 7x7 kerenl 사이즈를 사용했지만 ([Part Ⅴ. Best CNN Architecture] 8. ResNet [2] 참고), CIFAR-10의 영상은 크기가 매우 작기 때문에, 맨 처음 convolutional layer에 3x3 kernel을 썼다.
다음은 6n개의 3x3 convolutional layer 그룹이 온다. 6n 중 각각의 2n에 대하여 feature map의 크기가 {32, 16, 8}이 되도록 하였으며, filter의 개수는 연산량의 균형을 맞춰주기 위해 {16, 32, 64}가 되도록 하였다.
맨 마지막에 global average pooling과 10-way softmax를 배치하였으며, 결과적으로 전체 layer의 수는 “6n + 2”가 되었다.
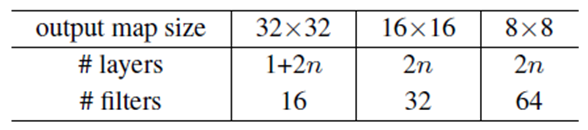
n = {3, 5, 7, 9}로 설정을 하면 20/32/44/56-layer를 얻을 수 있으며, 이것들에 대한 실험 결과는 다음 그림과 같다. ImageNet 데이터를 이용한 실험과 거의 동일한 양상의 결과를 보여준다.
Analysis of Layer Responses
Plain 망과 Residual 망에 대하여 각각의 layer에서의 response에 대한 표준 편차를 살펴보았다. 이 결과는 Batch Normalization은 실행을 하고 ReLU 및 addition은 실행하기 전을 비교한 것이며, 결과는 아래 그림과 같다. 이 그림 중 밑에 있는 그림은 표준편차를 크기 별로 다시 sorting한 결과이다.
이 결과를 보면, Residual 망의 response가 Plain 망에 비해 작다는 것을 확인할 수 있다.
Residual 망의 결과가 Plain 망의 결과에 비해서 표준편차가 작으며, 이 실험 결과를 통해 망의 response가 크게 흔들리지 않는 것을 확인할 수 있었으며, 결론적으로 이런 이유로 인해 망이 깊어졌을 때 Plain 망에서 발생하는 문제가 Residual 망에서는 적게 발생하게 된다.
Exploring Over 1000 layers
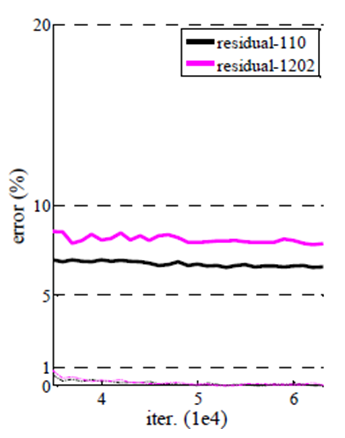
1202-layer network는 110-layer network와 유사한 training error 보였지만, 실제 성능은 더 좋지 못했다. 이는 overfitting의 문제로 보인다. dataset의 크기에 비해 layer가 불필요하게 많다는 것이 그 이유이다.
만약에 maxout, dropout같은 regularization을 쓴다면 성능이 향상되겠지만 이 paper에서는 dropout을 사용하지 않았다.
4.3 Object Detection on PASCAL and MS COCO
마찬가지로 recognition tasks에서도 빛을 발했다. COCO datasets에서 6.0% 더 높은 수치를 기록하였다, 이는 28%의 상대적인 발전이었다.
Reference












댓글남기기